|
ＳＤ閑話-６ 2010年9月2日 松本憲洋（POSY Corp.） タイトル：「クロマグロの漁獲と資源管理のシミュレーション」 ＳＤ閑話－５では、太平洋のクロマグロの漁獲量と資源量との関係を把握するために、その基本モデルとして傾向分析用の定量モデルを構築しました。 この閑話-６では、漁業関係者が操作可能な魚齢別の漁獲率などが、資源量などの成果変数にどのように影響するかをシミュレーションによって把握したいと思います。 これらは仮想操業における仮説検証を意味しており、いわゆる”戦略シミュレーション”と呼ばれている一部に相当します。 また、前の閑話で詳しくは触れませんでしたが、今回構築したモデルでは、成魚の資源が卵を産んで稚魚を生成しますから、モデル全体でレインフォーシング・ループを形成しています。 さらに、このループの構成要素は複雑な挙動をしますから、シミュレーション期間の20年間に変動要因の平均値が同じであっても、初期の時系列パターンの違いによって、その後の成果変数の結果は極端に違ってきます。 フィードバック・ループで構成されるシステムでは大変重要な問題ですから、変動の時系列パターンがシミュレーション結果にどのように影響するかについても 、本閑話の最後で現象的に説明しておきたいと思います。 １．基本モデル ”成魚当りの稚魚生存量”、”漁獲率１０”、”２－２０漁獲”および”世界の漁獲量推定”に正規分布の乱数を加えた基本モデルを以下に再録します。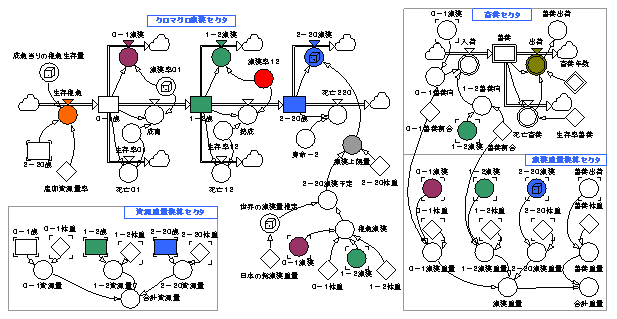  変動要因が加わる場合には、確率分布の特性が同じであっても、時系列パターンが違うとシミュレーション結果は大きく異なります。 閑話－５では触れませんでしたが、加えた乱数のSeedを以下に記します。 このランダム変数の時系列パターンの影響については、後の”４．変動パターンの影響”で説明します。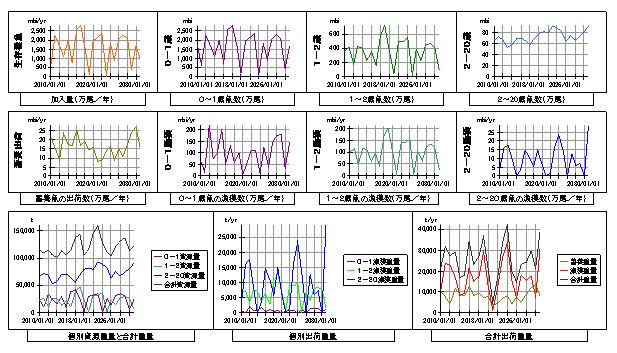 加えた乱数の定義 加えた変数名 分布形状 期待値 標準偏差 Seed 成魚当りの稚魚生存量 正規分布 １ 0.4 0.99 漁獲率１０ 正規分布 １ 0.4 0.3 ２－２０漁獲 正規分布 １ 0.4 0.4 世界の漁獲量推定 正規分布 １ 0.5 0.8 上記の乱数を加えた場合のシミュレーション結果を以下に再録します。 上記のように操作変数が確率変数として表現される場合には、本来は確率シミュレーションによって成果変数の統計結果を評価すべきです。 しかし、これは論文ではなく閑話ですから簡易的に以下のように考えています。 下記のシミュレーション結果におけるいずれもの変数が、時間経過に対してある一定の値の周りで変動しています。 これは、参照している文献に書かれている実際の状況によく似ています。 そこで、この均衡状態に、変更要素が加わった場合の成果変数の変化の様子を調べることにします。  ２．操作可能変数の影響 漁業関係者にとって、畜養を除けば、漁獲量だけが操作可能な要素になります。 前述のモデルでは、０から１歳魚の”漁獲率０１”、１から２歳魚の”漁獲率１２”および”日本の漁獲重量”がそれにあたります。 シミュレーション開始から５年後に、それぞれの漁獲率を単独で下表に記す量だけ増減させてシミュレーションを実施します。 操作変数名 基本モデルの設定 減少設定 増加設定 ”漁獲率０１” 7% 4% 10% ”漁獲率１２” 28% 27% 29% ”日本の漁獲重量” 13,400t/年 20%減 20%増 比較の基になりる基本モデルの設定によるシミュレーション結果を以下に示します。  （１）”漁獲率０１” 減少設定と増加設定によるシミュレーション結果を以下に示します。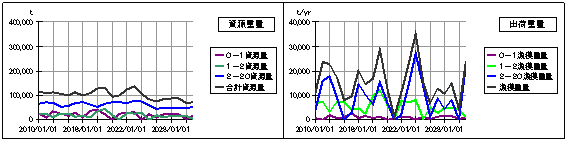   上図の漁獲率０１は3%で、漁獲量０１は120万尾/年から約50万尾/年だけ減少し、資源”１－２歳”に流入する”成育”は360万尾/年から50万尾/年だけ増えています。 その結果、漁獲高の変化は総体的には認められず、資源量が経過時間と共に漸増しています。 下図の漁獲率０１は10%で、減少させた場合と逆の現象が認められます。 しかし、両者の結果から、０から１歳の漁獲率を、基本モデルの7%に対して大きな割合で変更しても、漁獲高だけでなく資源量にも余り大きな影響が生じないと言えます。 （２）”漁獲率１２” 減少設定と増加設定によるシミュレーション結果を以下に示します。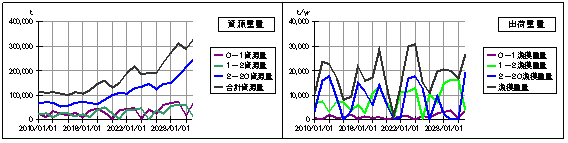   上図は漁獲率１２が、基本モデルの設定の28%よりわずかに1%だけ小さい27%です。漁獲高の変化は総体的には認められず、資源量は約３倍にまで増加しています。 この変更により１－２漁獲は101万尾/年から97万尾/年にわずか3から4万尾/年だけ減少し、その分が資源”２-20歳”に流入する”熟成”を13万尾/年から17万尾/年に押し上げています。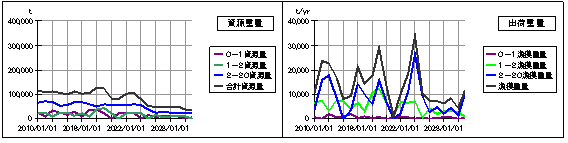 下図は漁獲率１２が、基本モデルの設定の28%より1%だけ大きい29%です。 資源量の変化は漁獲率１２を減少させた場合ほど極端ではありませんが明確に減少しています。また、漁獲高も減少しています。 結論として、漁獲率１２を減少させることで、漁獲高を減少させることなく、資源量を増やすことができることが分かります。 （３）”日本の漁獲重量” 減少設定と増加設定によるシミュレーション結果を以下に示します。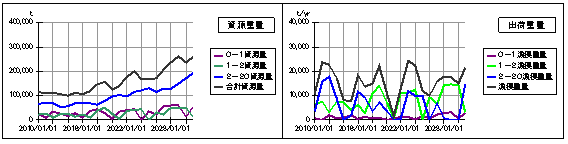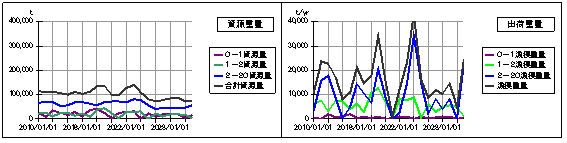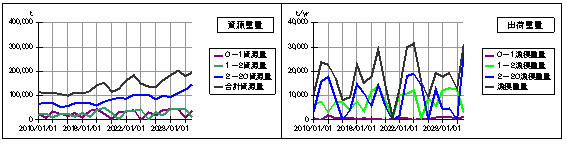   上図は日本の漁獲重量が20%減少した場合です。世界の漁獲量に対して日本の漁獲量は73%で変わらないとしていますから、結果として世界の漁獲量が減少することになります。 シミュレーション結果によっても基本モデルの結果に比べて、漁獲量が相対的に減少し、資源量の合計は２倍半まで増加しています。 一方、下図は日本の漁獲量を20%増加した場合ですが、漁獲高は相対的に増加し、それに伴い資源量も時間経過と共に漸減しています。 仮に今回のシミュレーションで想定したように、現時点で資源量と漁獲量がバランスしている状態なら、総漁獲量を規制することで資源量を確実に増やせる可能性はあります。 しかし、このやり方では漁獲量が直接減少するので、漁業関係者には好ましくなく、クロマグロの生態を考慮した前述の（２）の方が望ましいと思います。 ３．畜養との連携 世界でクロマグロの畜養を始める魚齢は海域と生態系の関係で様々のようですが、今回の基本モデルでは０から１歳魚の３年畜養と１から２歳魚の２年畜養とを想定しています。 出荷時点の魚の体重は50kgと仮定しています。 基本モデルでは、０から１歳魚の約45万尾/年（初期段階で０－１漁獲の38%）をひき綱とまき網で捕獲して、畜養の生簀に投入しています。 １から２歳魚は畜養に供しないことになっています。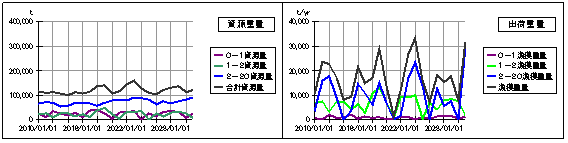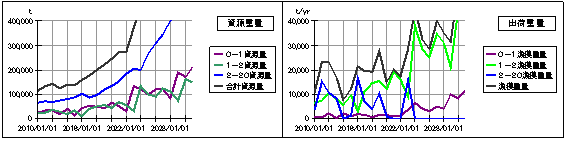 以上の条件でシミュレーションした畜養出荷量と漁獲出荷量などを以下に示します。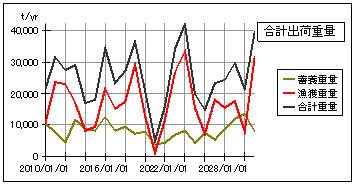  畜養出荷量は、1万トン／年弱で推移しています。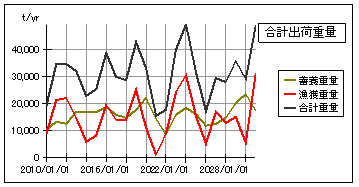 次に、１から２歳の”１－２漁獲”の30%を畜養生簀へ供するとした場合のシミュレーション結果を以下に示します。 シミュレーション開始時の１－２歳魚の漁獲高は約100万尾/年ですから、その30%である約30万尾/年を畜養生簀に投入し、２年後に50kg前後になったところで出荷することにします。 １－２漁獲の30%が食用になりませんので、（食用の）漁獲重量は年間2千トン程度減少します。 しかし、畜養重量が1万トン弱から2万トン弱まで増加するために、食用の漁獲と畜養出荷とを合わせた合計出荷重量は、2.5万トン程度から3万トン程度にまで大幅に増加します。 天然物と畜養物では味や価格の違いがありますが、量的には１－２漁獲を一部だけ畜養にまわすことで短期間のうちに供給量を増やすことができそうです。 なお、この例の資源量は、基本モデルの場合と同じです。  ４．変動パターンの影響 今回のモデルでは、参照した文献の内容から、クロマグロの漁獲量と資源量とは、時間ベースで変動しているが、その平均値は時間経過と共に大きな変化はなく、総合的には均衡状態にあると仮定しています。 その状態をモデルで実現するために、先ず、変動がない状態で、構成する要因の初期状態が時間が経過しても変化しないことを確認しました。 次に、そのモデルの4つの要素に、変動要因を加算しました。 その変動要因の選択において、20年間のシミュレーション結果に短周期の変動はあっても、長期的な平均の変化は生じないことと、変動振幅が参照した文献で発表されている値になるべく近くなることを選定条件にしました。 例えば、成魚当りの稚魚生存量の乱数の定義では、Seedは0.99でした。この値を0.9として、異なる時系列の乱数を適用してみましょう。 加えた変数名 分布形状 期待値 標準偏差 Seed 成魚当りの稚魚生存量 正規分布 １ 0.4 0.99 上図が基本モデルの結果で、下図が期待値と標準偏差をそのままにして、Seedを0.9とした場合の結果です。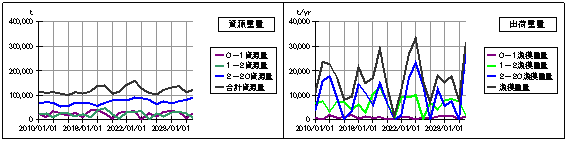   このときの二つの乱数を比較して以下に示します。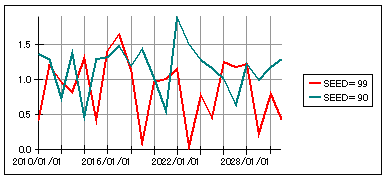  上記の乱数の時系列データから判断すると、このモデルの場合には、初期状態が1.0より大きいか小さいかで、その後の成果変数の挙動が極端に違ってきます。 これは、フィードバック・ループで増幅や減衰がなされるためですから、途中経過を見ながら目標の実現に向けた適応操作が必要になることを示唆しています。 また、最初でも述べましたように、今回は取り組みませんでしたが、確率変数に対する工学的な対応では、確率シュミレーションを実施して、特定の乱数パターンに対する挙動だけでなく、統計処理が可能となる 多数の乱数に対して挙動を求める必要があります。 ５．シミュレーションからの推論 参照した文献を真として検証もしないままに作成したモデルですから、確定的な結論を示すことができるわけではありません。しかし、実学においては、関係する要素を部分的に緻密に分析するだけでなく、このようにマクロ的に捉える必要があると考えています。 そのような目的に対して、システム・ダイナミックスによる傾向分析を目指した定量モデルは大いに効果的であることを、閑話－４／５／６で示したいと思いました。 したがって、モデリング＆シミュレーションの対象とした太平洋クロマグロについて、水産学の専門家でない私がとやかく言うのは関係者に笑止千万でしょうが、クロマグロに関する３本の閑話のまとめとして推論 の例を簡単にお話しします。 ただし、モデリング＆シミュレーションで取り上げた前提として、現状の漁獲量と資源量とが総合的にはバランスしていると仮定していることにご留意下さい。 （１）１から２歳魚の”漁獲率１２”をわずかに減少させて、１－２漁獲を3～4%減少させることで、合計の漁獲重量をほとんど変化させることなく、15年間で資源量を初期状態の ３倍程度まで増加させることができる。 そのために、まき網の魚体寸法による選別規制が有効と思われる。 （２）増加しているクロマグロの幼魚の内、１から２歳魚の漁獲量の一部を畜養にまわすことで、食用の漁獲量は減るものの、畜養出荷が増えるので、合計ではクロマグロの出荷量は増加する。 例えば、初期の１－２漁獲の30%である30万尾/年を畜養に回せば、漁獲高と畜養出荷高を合わせた合計出荷重量は、2.2トン／年平均から、3万トン/年平均まで増加する。 （３）０から１歳魚の”漁獲率０１”の増減は、合計漁獲重量や資源量に大きな影響を及ぼさない。 （４）卵から育てるクロマグロの養殖が長期間の研究開発の成果として完成したと聞いています。学問的には素晴らしい成果だと思います。 しかし、実用的な観点からは、漁獲した１から２歳魚の”１－２漁獲”を少しだけ畜養にまわせるように準備 できないでしょうか。 そうすれば、畜養の方が完全養殖より容易でしょうし、自然環境に比べて死亡率を低く抑えてることができるでしょうから、蓄養を拡大する方が、養殖の実用化より現実的 な対処法と言えるのではないでしょうか？
読者の皆様も閑話－５の終わりの部分で、クロマグロのモデルをダウンロードできますから、ダウンロードしたモデルの構造や係数を変えながら、諸々の仮説をシミュレーションで検証して、傍目八目の推論を立ててみませんか。システム・ダイナミックスが複雑な問題を解決するための方法論として、有効であることをきっと実感していただけることでしょう。
ダウンロードの方法 ① http://www.posy.co.jp/PS-download-f.htm を開く。 ② 上端の“評価版のダウンロード”をクリック。 ③ ■評価版：Studio Express のダウンロードにある空色のボックスをクリックすると、Powersim社のダウンロードのページに入りますから指示に沿って進んでください。 Studio 8 Expressの機能 ▼再インストール：繰り返し可能 ▼機能：商品版と全く同一機能（具体的には、その時点で最新のProfessional版） ▼要素数：50以下 ▼有効期間：Powersim社がメールでプロダクト・キィを送付した後６０日間
ＳＤ閑話-６ 了 |
